Pika
Сообщение
#75477 2.6.2011, 10:07
Необходимо вычислить поверхностный интеграл второго рода

Понимаю,что нужно разбить на сумму трёх интегралов,но каким способом их вычислять идей нет,а так же не понимаю,что есть
нижняя сторона части параболоида..помогите с решением,пожалуйста
Тролль
Сообщение
#75479 2.6.2011, 10:58
А как вычисляются поверхностные интегралы второго рода знаете?
Pika
Сообщение
#75481 2.6.2011, 11:08
Тролль,не могу в этом разобраться как раз..описание и примеры читаю,но не могу понять как найти
направляющие косинусы нормали и что с ними делать дальше

Pika
Сообщение
#75508 2.6.2011, 14:29
Можно ли с помощью формулы Остроградского перейти к такому виду

,где D заданная область??

Тролль
Сообщение
#75520 2.6.2011, 20:44
Pika
Сообщение
#75551 3.6.2011, 14:45
Тролль ,оттуда "вдохновение" и черпал..но ничего так сделать и не смог
Тролль
Сообщение
#75556 3.6.2011, 17:37
Пример 5.
x = r * cos fi, y = r * sin fi, z = r^2.
Pika
Сообщение
#76100 21.6.2011, 10:23
Тролль ,а почему именно такая замена??

И если подставлять в
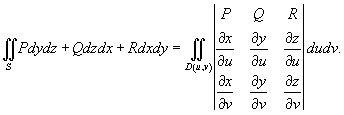
,то как дифференцировать,ноль же выходит

Тролль
Сообщение
#76115 22.6.2011, 7:40
Это полярная система координат. А как получился 0?
Pika
Сообщение
#76116 22.6.2011, 8:50
Тролль,ну,что полярная я понял..получается дифференцировать надо по r и fi (вместо u и v,в случае приведенной выше формулы)??
Тролль
Сообщение
#76117 22.6.2011, 10:34
Ну да.
Pika
Сообщение
#76129 23.6.2011, 15:46
Посчитал,выходит вот так..

и как это теперь лучше разделить,для удобности счёта??

Тролль
Сообщение
#76138 24.6.2011, 6:21
Что-то непонятные какие-то знаки. Что за знак "не равно"?
Pika
Сообщение
#76139 24.6.2011, 7:15
Тролль,это *,тобишь умножить..
r^5(+cos^2(fi)sin^2(fi)-2r^3*cos^7(fi)-2r*sin^5(fi))..вот это выходит
Тролль
Сообщение
#76140 24.6.2011, 10:13
Должно получиться
r^5 - 2r * (r^7 * cos^7 fi + r^5 * sin^5 fi)
Этот интеграл уже легко считается.
Pika
Сообщение
#76141 24.6.2011, 11:00
Тролль,премного благодарен
Это текстовая версия — только основной контент. Для просмотра полной версии этой страницы, пожалуйста,
нажмите сюда.


 ,где D заданная область??
,где D заданная область?? 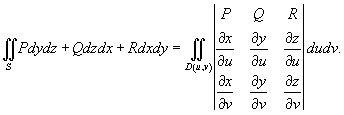 ,то как дифференцировать,ноль же выходит
,то как дифференцировать,ноль же выходит 