2 -1 1
А=-1 2 1
0 0 1
Сделано: нашел собственные числа лямбда1=1 и лямбда2=2, далее как делать не понятно.
рассматриваем случай для Л1=1, да? получается красивая матрица
1 -1 1
0 0 0
0 0 0
И все! финиш! Посмотрел пример, там красота: Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их" и ответ! Все очевидно и не понятно
воо, нашел еще пример(тыц) в котором не понятно это-
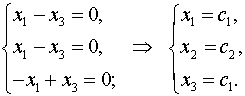
как получилась первая система ясно, но вот дальнейший переход...
