Помогите решать, корни нашёл а вот дальше незнаю как
Фото
Полная версия: y''-4y=(24e^2x)-4cos2x+8sin2x > Дифференциальные уравнения
Помогите решать, корни нашёл
неправильно нашли
Цитата
а вот дальше незнаю как
Посмотрите здесь и далее примеры.
Практические:
yo=C1e^(2x)+C2e^(-2x)
yo=C1e^(2x)+C2e^(-2x)
Забыл поставить индекс нужный,
вот во всех уравнениях правая часть на примерах в стиле "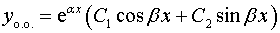
А как у меня выглядит будет, нигде не могу найти
вот во всех уравнениях правая часть на примерах в стиле "
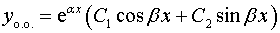
А как у меня выглядит будет, нигде не могу найти
я чёто не допер как мы так корни получили?
там же
y^2-4y=0
а не y^2-4=0
там же
y^2-4y=0
а не y^2-4=0
Там y^2 - 4 = 0
ну может я так коряво пишу, но там y^2-4y=0
Цитата
Там, это где?
Эм, ну в частной производной высшего порядка
да я спутал тематику, в дифф уравнении.
там корни 4 и 0
y^2-4y=0
там корни 4 и 0
y^2-4y=0
Цитата
Вам же уже неоднократно писали, что характеристическое уравнение не такое.
Спасибо, понял
Самое интересное решал с корнями 4 и 0
и мне препод сказал, правильно_
вроде как решил

и мне препод сказал, правильно_
вроде как решил

В данном уравнении корни действительно равны 0 и 4, а в первом уравнении 2 и -2.
Всё верно, осталось ответ записать.
Всё верно, осталось ответ записать.
Да да записал, на обороте и сдал, в четверг должен узнать 
Это текстовая версия — только основной контент. Для просмотра полной версии этой страницы, пожалуйста, нажмите сюда.

