При использовании элементарных преобразований по строкам матрица приходит к виду который сложно считать ступенчатым или треугольным. Я правильно понимаю что путем преобразований я никак не получу из этой системы уравнения треугольную матрицу???




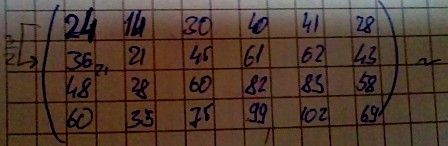
Помогите разобраться.

Это и есть треугольная матрица.

Не обязательно треугольную, вам надо привести к ступенчатой матрице.

Вопрос есть способ которым я смогу простить 1-ую строку матрицы?



все ли верно или еще как-нибудь можно разложить?

не поняла, еще раз вопрос?

Ну я имел ввиду, нужно ли проводить еще какие-либо операции, дабы решение СЛАУ методом Гаусса БЫЛО!
к примеру могу ли я первую строку матрицы упростить путем умножения 4-ой строки исходной матрицы на 0,4 и сложением с первой строкой. В конечной итоге я хочу получить матрицу оного вида.
(красными чернилами)

Приведение к ступенчатому виду - это и есть метод Гаусса.

Можете. Это преобразование относится к элементарным операциям над строками матрицы.